|
I view the central theme of this book as being
neither jungle travelogues nor even mathematics, but the philosophical question of
what mathematical proof consists of, the essential nature of mathematical/logical
truth itself and how people come to recognize it. I thought a lot about this sort
of thing back in my university days (ancient times!) so this was right up my alley!
I very much appreciated many of Mazur’s comments,
such as that while mathematics enjoys a reputation for being logically perfect, in
reality the truths of mathematics “are not communicated through airtight chains of
logical arguments” (p. x), and his statement that “the whole notion of proof in
mathematics has never been clearly defined” (p. 38). There are in fact a fair number
of quite profound statements in Mazur’s book that a casual reader might not even
notice, such as that “We become so accustomed to what we believe that we cannot
believe otherwise” (p. 49) and “The mind has a big task: to interpret perceptions of
the world so that it can live without contradiction” (p. 44). I like books
that say things like this!
On the other hand, there are quite a lot of things
in Mazur’s book that I strongly disagreed with, some of which really made me cringe!
On p. 61 he seems to suggest that mathematicians must either be Platonists or
constructivists, but I reject both views. (One can accept the law of the excluded
middle without being a Platonist!)
Much of Mazur’s book is amenable to a materialist
interpretation, but he is far from being consistent on this. On p. 83, while discussing
non-Euclidean geometry, he remarks that instead of trying to prove Euclid’s fifth
postulate “we should have been celebrating the liberation of mathematics from the
physical world”. The fact remains, however, that mathematics has been mostly created
by abstracting from relationships of things in the real world, and that even
non-Euclidean geometries can be interpreted that way (as the surface geometry of
spheres or saddles). Yes, once we have abstracted a world of mathematical objects we
can sometimes manipulate them in ways divorced from actual reality. But the connection
of mathematics to the real world is still primary and is of deep significance. We
should perhaps be more inclined to lament “the liberation of mathematics from
the physical world” than to “celebrate it”!
Mazur has the irritating practice of referring to
things which are merely internally consistent as “true” (cf. p. 85). This is
a Platonist vice. Poincaré was indeed correct to say “One geometry cannot be
more true than another; it can only be more convenient.” But this should be taken to
mean that it is only correct to call any geometry (or any other branch of mathematics)
“true” only insofar as it is applicable to describing some aspect of the real world.
Thus even 1 + 1 = 2 is not always true when it comes to describing the physical
world. (E.g., one liter of water plus 1 liter of ethanol makes slightly less than 2
liters of water-alcohol mixture—because the molecules somewhat fit between each
other.)
On pages 66-69, in the very interesting discussion
of whether “Behold!” demonstrations in mathematics can actually constitute “proofs”,
I thought Mazur went somewhat astray. My view is that what constitutes an adequate
“proof” depends on both the evidence or arguments presented and on how
well prepared the person is to understand that evidence and those arguments. For me
the following illustration (from p. 66) does prove the theorem that the sum of
any list of sequential odd numbers starting with 1 must be a square number, and it
proves it at least as well as any verbal or algebraic argument could!:
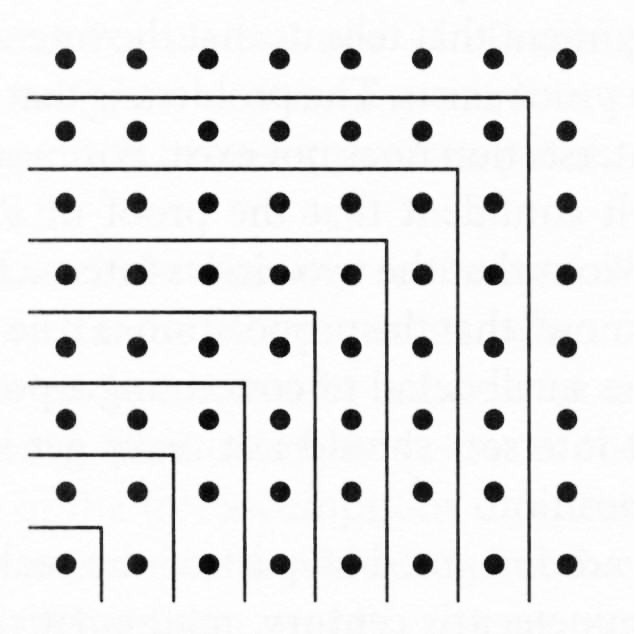
A example “Behold!” proof.
I grant, however, that there are reasons to favor
an algebraic proof here, and that is the accepted standard for a proof of this kind
of thing within the mathematical community. As Mazur appropriately remarks in other
places, mathematicians have their own accepted standards of proof which are not,
however, entirely precise and completely logical demonstrations, but rather merely
enough in that direction so that most mathematicians in that particular field
will recognize it as sufficient. Moreover, the typical procedure is for mathematicians
to hide how they actually came to understand and prove the conclusion to their
own satisfaction, by making the published “proof” more logical and complete than their
real method of arriving at it! As another mathematician once wrote, “Our paper became
a monograph. When we had completed the details, we rewrote everything so that no one
could tell how we came upon our ideas or why. This is the standard in
mathematics.”1
I would concede that sometimes “Behold!” proofs are
sufficient to convince someone, and sometimes they aren’t, and it may vary with the
specific person. And in many cases they perhaps only suggest that something is
true.
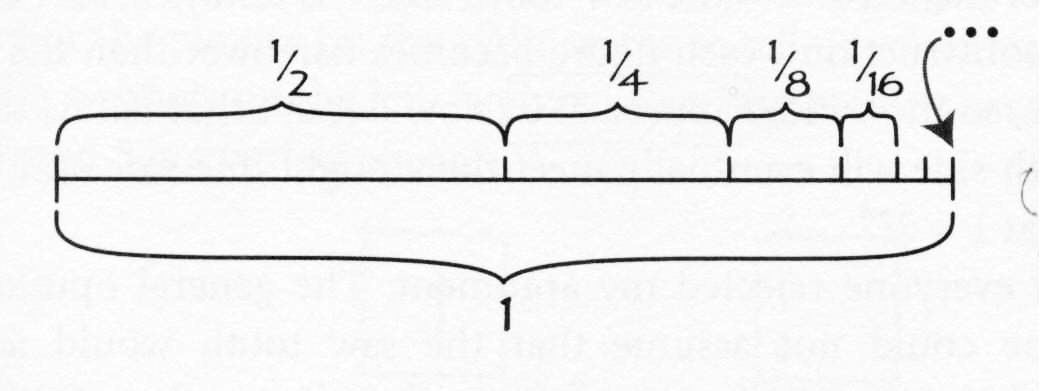
A “Behold!” proof that the sum of all fractions of the form
(1/2)n (where n is a positive integer) equals one.
However Mazur goes on to argue (pp. 67-68) that “If
anyone believes that the last picture proves that the sum of the fractions (1/2)n
equals 1, then I have a picture that proves that 1 = 2.” But to my mind his sequence of
pictures on p. 69 proves no such thing!2 A lot depends
upon how one is prepared to interpret such “Behold!” illustrations. And a prepared
mind is always the key to the correct understanding of anything. Moreover, it is not just
the “Behold!” sort of “proofs” that can turn out to be fallacious; this can also happen
with algebraic or any other form of mathematical proof.3
There were many things of interest in the book, such
as the young boy Evan’s own explanation of how he solved the bullseye puzzle (pp. 98-100).
But I thought that there were weaknesses in the discussion of infinity and probability,
such as too much acquiescence toward the false idea that infinity is inherently mystifying.
The book often seemed to be on the right track philosophically, but then veered off in one
way or another. This is why, even though I enjoyed the book, I only give it a 7 instead of
a 10.
The book could have benefitted from another round of
proofreading. The worst error I spotted was on p. 296 where the formula for the sum of the
first n integers is given as ((n+1)+1)/2 when in fact it is (n(n+1))/2.
|


